We are mainly dealing with applied mathematics: we develop and employ mathematical approaches, methods and tools to investigate issues and questions which arise in different fields, from socio-economic ones to engineering and technological ones. Our research includes the various stages of modelling, analytical study and numerical simulations.
A few keywords are associated below to each of us.

BERTOTTI Maria Letizia
Mathematical models for complex systems
Structure and properties of complex networks
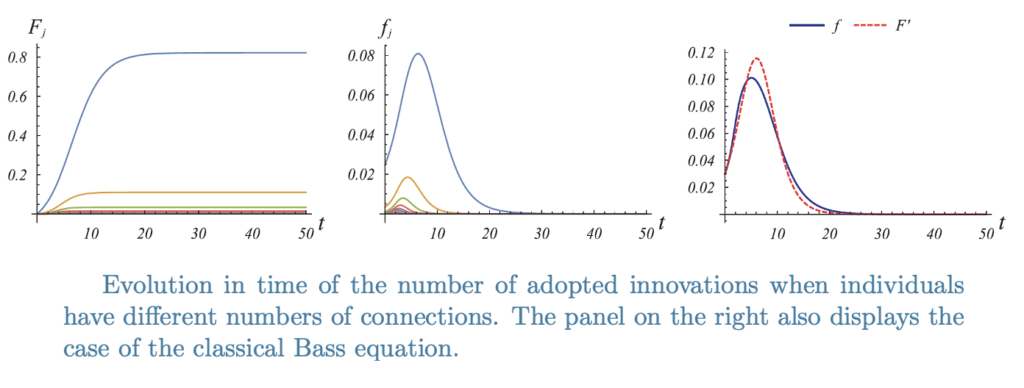
Diffusion dynamics on top of complex networks
Mathematical models for socio-economic systems
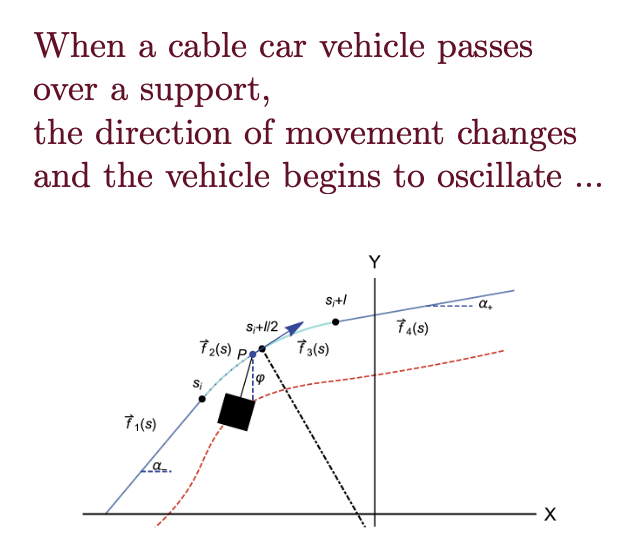
Equations and simulations of ropeway dynamics

COLOMBARO Ivano
Fractional calculus and linear viscoelasticity
Prabhakar fractional calculus
Exterior calculus and generalized electromagnetic models

LEVAGGI Laura
Non-cooperative game theory with applications to economics
Optimality and welfare analysis of regulatory policies
Variable structure control

MODANESE Giovanni
Mathematical models for complex systems
Structure and properties of complex networks
Diffusion dynamics on top of complex networks
Theoretical physics: field theory, quantum systems
Equations and simulations of ropeway dynamics
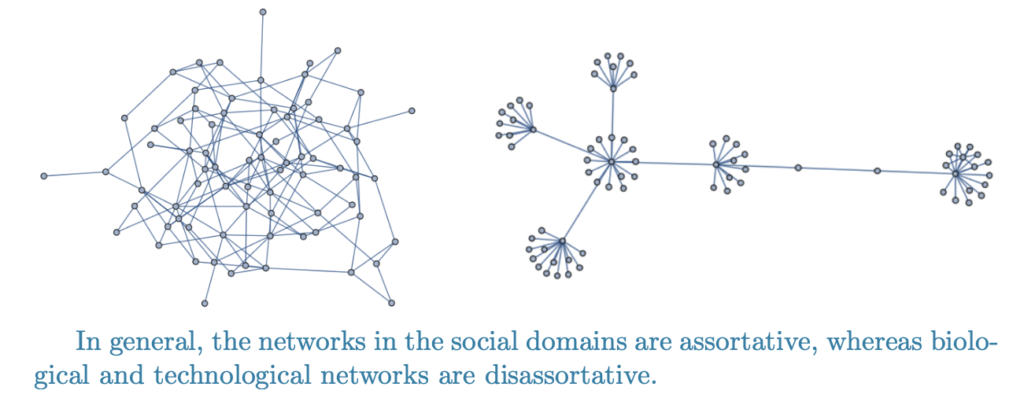
Structure and properties of complex networks
Equations and simulations of ropeway dynamics
Diffusion dynamics on top of complex networks
Optimality and welfare analysis of regulatory policies
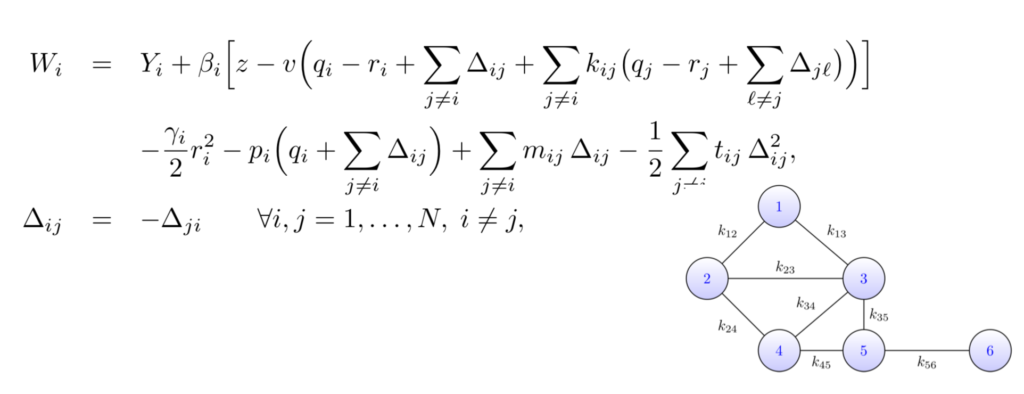
Prabhakar fractional calculus